[Hexlet] JS: Деревья

Andrew.Kaluba · 09.Декабрь.2018 10:10:50

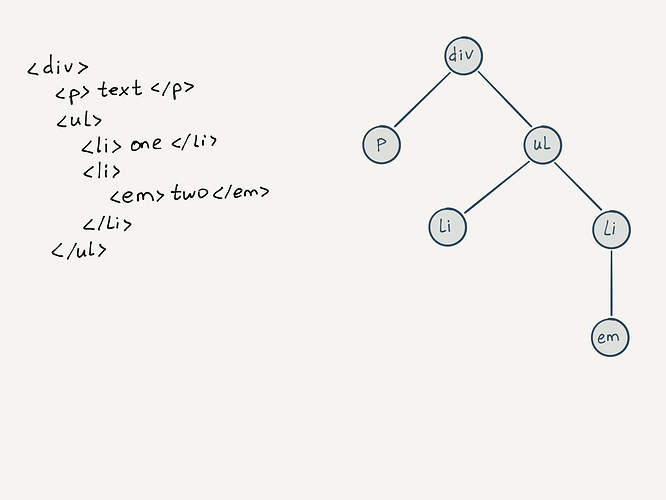
Дерево — одна из самых распространённых структур данных в информатике и естественный способ моделирования некоторых предметных областей. С деревьями (как структурой данных) встречаются так или иначе все люди, даже те, кто далёк не только от программирования, но и от компьютеров в целом. Самым очевидным примером служит генеалогическое дерево , а из более специализированного — файловое дерево . Ну и, конечно, HTML (а так же json , xml и многое другое), он также имеет древовидную структуру. Любая иерархия является деревом по определению.

С деревьями связан один очень интересный аспект. Я часто наблюдаю, как уровень понимания темы деревьев и способность с ними работать невероятно сильно коррелирует с уровнем разработчика. Многие дальнейшие курсы на Хекслете в своих проектах используют деревья на полную катушку.

В этом небольшом курсе мы слегка погрузимся в тему деревьев и научимся с ними работать. Материал текущего курса логически продолжает тему коллекций . Рассматриваемые темы аналогичны: определение, обход, отображение, поиск, агрегация (reduce). На практике это означает, что мы перейдём от линейной к древовидной рекурсии.

Чего не будет в этом курсе, так это алгоритмов в том виде, в котором эта тема подаётся в университете. Наша задача ухватить концепции и выйти на новый уровень абстракции, а не выиграть олимпиаду Но если эта тема вам интересна (надеюсь, что да!), то в нашем списке рекомендуемой литературы, вы найдёте отличную книгу, посвящённую алгоритмам.

JS: Деревья → Определения

Ключевая черта древовидной структуры в том, что она рекурсивна . Другими словами, дерево состоит из поддеревьев, которые в свою очередь состоят из поддеревьев, которые в свою очередь… В конце концов, в самом низу, находятся листья — и вот они уже не имеют потомков и никуда не ведут.

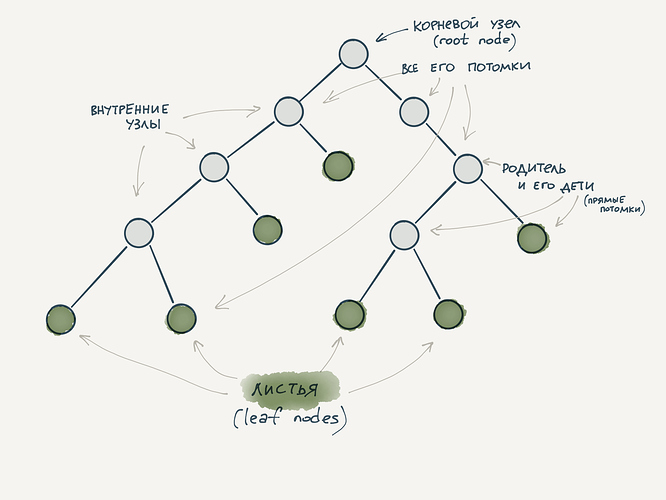
Дерево состоит из узлов (вершин или нод, так как по-английски узел — это node ) и рёбер между ними. Рёбра в реальности не существуют, они нужны лишь для того, чтобы визуализировать связь и, по необходимости, описать её. Узлы делятся на два типа: внутренние (те, у которых есть потомки) и листовые узлы (те, у которых нет потомков). В случае файловой системы листовые узлы представлены файлами, а внутренние — директориями.

В деревьях у каждой вершины есть родитель (или предок). Единственным исключением является корневой узел — у него нет родителей, и именно с него начинается дерево. Количество потомков у любой внутренней вершины, в общем случае, может быть любым. Кроме того, в деревьях выделяют понятие глубины (depth), определяющей то, сколько шагов нужно пройти по вершинам от корневой, чтобы достичь текущей (той, на которую смотрим). Вершины на одной глубине с общим родителем называют братскими или сестринскими.

Определение

Количество способов, которыми можно описать деревья, бесконечно много. Здесь мы рассмотрим только те, которые основаны на повторении структуры дерева в той структуре данных, которая его описывает. Самый примитивный вариант — это вложенные массивы:

[[1, 4], 2, [3, 8]];
//     *
//    /|\
//   * 2 *
//  /|   |\
// 1 4   3 8

[3, 2, [3, 8], [[8], 3]];
[1, null, [[3]], [5, 'string', [undefined, [3], { key: 'value' }]]];

В примерах выше корень — это сам массив, а все его элементы — это дети. Если ребенок не является массивом, то он рассматривается как листовой узел, иначе — как внутренний узел. Внутренний узел, в свою очередь, состоит из детей. Такая структура имеет ограничение. Внутренние узлы не могут хранить данных, но, в целом, такая схема может использоваться и встречаться в жизни.

Можно пойти дальше и добиться большей гибкости . Представим каждый элемент дерева массивом, в котором первый элемент — это значение, хранящееся в узле, а второй элемент — массив детей. Если второй элемент отсутствует, то считаем, что текущий узел — листовой.

[[3], [4], [[10], [[3], [2], [8], [[2], [[3], [4]]]]]]

Такой вариант многословнее, но позволяет хранить данные (произвольные) в любом узле, даже не листовом. Теперь, надеюсь, вам понятен принцип организации, и вы можете самостоятельно попрактиковаться в придумывании способов упаковки деревьев в массив. Кстати, интересная деталь. Исходный код высокоуровневых языков тоже имеет рекурсивную структуру. Посмотрите на код:

f1(3 * f2(f3() + 5));

Аргументы функции — выражения, а значит могут быть вызовами функций, что порождает рекурсию. Если код выше переписать в стиле lisp языков, то получится самое настоящее дерево, состоящее из списков:

(f1 (* 3 (f2 (+ 5 (f3))))

Соглашение здесь такое: первым элементом списка является функция (любые операции рассматриваются как функции), а всё остальное — её аргументы.

Ещё один способ определения основан на ассоциативных массивах, а конкретно в javascript — на объектах:

{
  value: 5,
  children: [
    { value: 10 },
    { value: 100 },
    { value: 'nested', children: [/* ... */] }
  ]
}

По большому счету, что массив, что объект сами по себе всегда могут рассматриваться как дерево, безотносительно своей внутренней структуры и наличию вложенных элементов. Такова их природа. Структура присутствует там, где нужно хранить именно древовидные данные, например, файловую систему. Начну с того, что открою секрет, большинство файловых систем не просто имеют древовидную структуру, но и на уровне реализации представлены деревьями как структурами данных.

По ходу курса мы будем работать с одной и той же структурой, создавая поверх неё различные вспомогательные функции для поиска и модификации содержимого. Ниже показан код (dsl), который создаёт необходимый объект-дерево:

const tree = mkdir('etc', [
  mkdir('consul', [
    mkfile('config.json', { size: 1200 }),
  ]),
], { key: 'value' });

В результате выполнения кода получается следующий результат:

{
  name: 'etc',
  type: 'directory',
  meta: {
    key: 'value',
  },
  children: [
    {
      name: 'consul',
      type: 'directory',
      meta: {},
      children: [
        {
          name: 'config.json',
          type: 'file',
          meta: {
            size: 1200
          }
        }
      ],
    },
  ],
};

Представление директории:

{
  name: /* ... */,
  type: 'directory',
  meta: {},
  children: [/* ... */],
}

Представление файла:

{
  name: /* ... */,
  type: 'file',
  meta: {},
}

Некоторые утверждения относительно дерева выше:

Файлы — листовые узлы
Директории — внутренние. Могут содержать как файлы, так и директории внутри свойства children
meta — объект с произвольными данными, например, размером, датой создания и так далее
Директорию от файла отличает, в первую очередь, тип , заданный соответствующим свойством

Про последнее скажу пару слов. То самое понимание ООП, о котором так много говорят, как раз заключается в том, что код рассматривается с точки зрения типов, и вы их можете увидеть. Важно выделять их явно, а не анализировать по косвенным признакам — например, определение того, что за нода перед нами (какой у неё тип!), нужно делать через проверку type , а не через проверку наличия свойства children .

JS: Деревья → Traversal

Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева . Подразумевается, что в процессе обхода каждый узел будет затронут только один раз. По большому счету, все так же, как и в обходе любой коллекции, используя цикл или рекурсию. Только в случае деревьев способов обхода больше, чем просто слева направо и справа налево. В данном курсе используется один порядок обхода — обход в глубину , так как он естественным образом получается при рекурсивном обходе. Об остальных способах можно прочитать на википедии либо в рекомендованных книгах Хекслета.

Обход в глубину (Depth-first search)

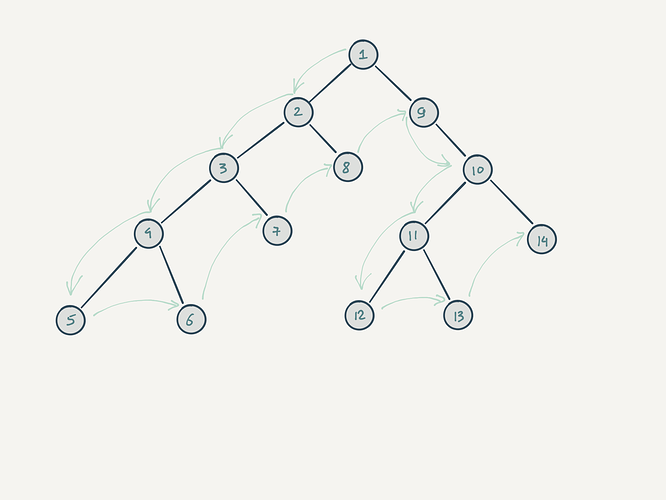
Один из методов обхода дерева (графа в общем случае). Стратегия этого поиска состоит в том, чтобы идти вглубь одного поддерева настолько, насколько это возможно. Этот алгоритм естественным образом ложится на рекурсивное решение и получается сам собой.

Рассмотрим данный алгоритм на примере следующего дерева:

//     * A
//    /|\
// B * C * D
//  /|   |\
// E F   G J

Каждую нелистовую вершину я обозначил звёздочкой. Обход начинается с корневого узла.

Проверяем, есть ли у вершины A дети. Если есть, то запускаем обход рекурсивно для каждого ребёнка независимо.
Внутри первого рекурсивного вызова оказывается следующее поддерево:

// B *
//  /|
// E F

Повторяем логику первого шага. Проваливаемся на уровень ниже.

Внутри оказывается листовой элемент E . Функция убеждается, что у узла нет дочерних элементов, выполняет необходимую работу и возвращает результат наверх.
Снова оказываемся в ситуации:

// B *
//  /|
// E F

В этом месте, как мы помним, рекурсивный вызов запускался на каждом из детей. Так как первый ребёнок уже был посещён, второй рекурсивный вызов заходит в узел F и выполняет там свою работу. После этого происходит возврат выше, и всё повторяется до тех пор, пока не дойдёт до корня.

JS: Деревья → Map

Пример предыдущего урока крайне просто обобщить до функции высшего порядка map . Напомню, что map — отображение . Если раньше мы отображали плоские списки, то теперь отобразим вложенную структуру. С точки зрения семантики ничего не меняется. map каждому узлу ставит в соответствие новый узел, так что структура всего дерева остаётся прежней, а вот данные внутри узла меняются.

JS: Деревья → Filter

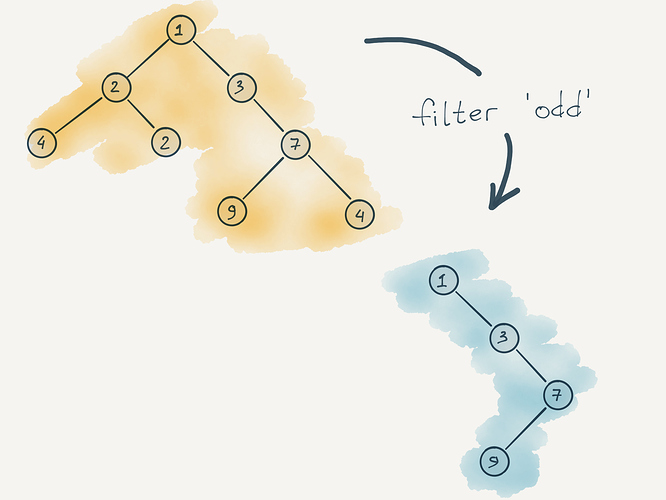
В отличие от map , filter для деревьев, в том виде в котором он используется для коллекций, практически непригоден. Посудите сами. Предположим мы хотим выполнить поиск по файловой системе файлов подходящих под шаблон *.log . Задача сразу разбивается на две подзадачи. Фильтрация оставляющая листовые узлы и последующая фильтрация по шаблону. Очевидно что после первого фильтра, мы уже хотим работать со списком, но никак не с деревом. Более того, как будет выглядеть дерево в котором только одни файлы и какой в нем практический смысл? Как ни крути, большинство фильтров древовидных структур, должны на выходе давать плоские списки.

Но все же иногда, filter может использоваться, к тому же, для полноты картины, стоит пройти все шаги. Для начала необходимо определиться с тем что нужно вернуть в ситуации если нода не удовлетворяет предикату. Логично использовать null .

//   a *
//    /|\
// B * C * d
//  /|   |\
// e  F  G j

Глядя на реализацию фильтра, видно что если нода не удовлетворяет предикату, то ее дети не рассматриваются вообще. В примере выше это нода B . Соответственно ее дети e и F даже не анализируются и отфильтровываются вместе с B .

Интересно выглядит и вот эта запись children.map(c => filter(f, c)).filter(v => v) . Дело в том что наш фильтр, не работает со списком, а работает с конкретным корневым узлом. Соответственно если мы обрабатываем детей, то в результате фильтрации количество детей не уменьшается. На их месте появляется null . Поэтому обход детей совершается используя map на массиве children с последующим filter . Тогда все null элементы отфильтруются.

JS: Деревья → Reduce

reduce , пожалуй, самая интересная и полезная функция для работы с деревьями. Агрегация данных — операция, встречающаяся крайне часто. Подсчитать число файлов в папке, общий вес всех файлов в папке, получить список всех файлов в папке, найти все файлы по шаблону, все это удобнее сделать с помощью reduce .

Главная особенность reduce в наличии аккумулятора, который протаскивается сквозь все вызовы до самой глубины, а затем поднимается наверх и, в конце концов, возвращается наружу.

Выше пример теста, в котором используется reduce для подсчета количества узлов в дереве. С помощью reduce , задача выполняется в одну строку.

Так же как и в остальных функциях высшего порядка, в функцию обработчик передается нода целиком, а не только имя. Самое интересное происходит при обработке детей. Вызов reduce на каждом ребенке должен происходить с аккумулятором, протаскиваемым сквозь обработку каждого ребенка. Из-за этого получается что снаружи есть reduce перебирающий children , в то время как каждый ребенок принимает на вход текущий acc внешнего reduce и запускает внутренний с этим аккумулятором.

JS: Деревья → Поиск

Поиск по файловой системе - операция, выполняющаяся крайне часто. Она открывает большой простор для интересных задачек. Разберем одну из них с несколькими вариациями. Предположим, что мы хотим вывести список всех пустых директорий. Используя reduce , выполнить данную задачу тривиально. Возьмем следующую файловую структуру:

import { mkdir, mkfile } from 'hexlet-immutable-fs-trees';

const tree = mkdir('/', [
  mkdir('etc', [
    mkdir('apache'),
    mkdir('nginx', [
      mkfile('nginx.conf'),
    ]),
    mkdir('consul', [
      mkfile('config.json'),
      mkdir('data'),
    ]),
  ]),
  mkfile('hosts'),
  mkfile('resolve'),
]);

В этой структуре две пустых директории: /etc/apache и /etc/consul/data . Алгоритм поиска примитивный:

Инициализируем reduce массивом
Если тип ноды directory и у нее нет детей - добавляем в массив

import { reduce } from 'hexlet-immutable-fs-trees';

const dirs = reduce((acc, n) => {
  if (n.type === 'directory' && n.children.length === 0) {
    return [...acc, n.name];
  }
  return acc;
}, tree, []);

В этом примере раскрывается вся прелесть функций высшего порядка. От нас полностью скрыт механизм обхода дерева, более того, можно даже не знать, что мы работаем с деревом.

Попробуем усложнить задачу. Найдем все пустые директории, но с максимальной глубиной поиска 2 уровень. То есть пустая директория /etc/apache подходит под это условие, а вот /etc/consul/data - нет. Навскидку можно сразу назвать следующие способы решения:

Так как наша реализация reduce не предоставляет информацию о том, на какой глубине текущая нода, то можно выполнить обход вручную, передавая два аккумулятора: один с итоговым массивом, второй с уровнем вложенности.
Можно расширить само описание дерева, добавив туда информацию об уровне вложенности. С одной стороны, такой способ не потребует изменения прикладного кода, так как достаточно изменить реализацию интерфейсных функций mkdir и mkfile . С другой, в такой схеме глубина всех нод будет посчитана относительно корня, что неудобно.
Можно написать reduce которому можно сказать насколько глубоко идти. А затем решить задачу с его использованием.

Попробуем решить эту задачу, используя первый способ.

const findEmptyDirsDepth = (root, depth = 1) => {
  const iter = (n, currentDepth, acc) => {
    if (n.type === 'file' || currentDepth > depth) {
      return acc;
    }

    if (n.children.length === 0) {
      return [...acc, n.name];
    }
    return n.children.reduce((cAcc, nn) => iter(nn, currentDepth + 1, cAcc), acc);
  };

  return iter(root, 1, []);
};

const dirs = findEmptyDirsDepth(tree, 2);

Несколько важных моментов:

Теперь нужно отслеживать текущую глубину, поэтому она передается в iter , с каждой итерацией увеличиваясь на единицу.
Если зашли глубже, чем надо, то возвращаем результат.

В остальном код такой же, как и в обычном reduce .

JS: Деревья → Агрегация

Попрактикуемся еще с одним вариантом агрегации данных на файловых системах. Напишем функцию, которая принимает на вход директорию и возвращает список директорий первого уровня вложенности и количество файлов в них включая все поддиректории. Эта функция затем может использоваться в утилите командной строки выполняющей соответствующую задачу.

Как видно из постановки, задачу нельзя решить используя reduce в чистом виде, так как нам не нужен обход всех нод, с другой стороны для подсчета количества файлов обход нужен. Следовательно наша задача распадается уже на две подзадачи: извлечение детей-директорий текущего корня и вызов подсчета файлов внутри каждого ребенка.

Начнем с подсчета количества файлов. Эта задача содержит один примитивный reduce :

import { reduce } from 'hexlet-immutable-fs-trees';

const calculateFilesCount = tree =>
  reduce((acc, node) => (node.type === 'file' ? acc + 1 : acc), tree, 0);

Совершенно типичный reduce который увеличивает аккумулятор на единицу если тип ноды file . Следующий шаг заключается в том чтобы извлечь всех детей из исходного узла и к каждому из них применить подсчет.

import { mkdir, mkfile } from 'hexlet-immutable-fs-trees';

const tree = mkdir('/', [
  mkdir('etc', [
    mkdir('apache'),
    mkdir('nginx', [
      mkfile('nginx.conf'),
    ]),
  ]),
  mkdir('consul', [
    mkfile('config.json'),
    mkfile('file.tmp'),
    mkdir('data'),
  ]),
  mkfile('hosts'),
  mkfile('resolve'),
]);

const result = tree.children
  .filter(n => n.type === 'directory')
  .map(n => [n.name, calculateFilesCount(n)]);

console.log(result);
// => [['etc', 1], ['consul', 2]]

То есть мы обратились к детям напрямую сначала отфильтровав их, а затем и выполнив отображение на необходимый массив, содержащий для каждой директории имя и количество файлов в нем.